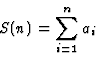
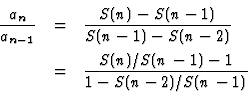
kde p, q, r jsou polynomy v n a platí
je polynom vyhovující
p(n)=q(n+1)f(n)-r(n)f(n-1).
(S(n),b):=GOSPER( a(n))
[předpokládá, že a(n)/a(n-1) je racionální lomená funkce,
pokud S(n)/S(n-1) je také racionální funkce je b=true
a S(n) je spočítáno, jinak b=false
použité algoritmy:
num(a) - čitatel racionální lomené funkce a
den(a) - jmenovatel racionální lomené funkce a
Res(x,p,q) - resultant polynomů p, q podle proměnné x
gcd(p,q) - největší společný dělitel polynomů p, q
deg(p(n)) - stupeň polynomu p(n)
cof(p(n),i) - koeficient u i-té mocnimy n v polynomu p(n) ]
1. b:=true;
2. if a(n)=0 then S(n):=0; return fi;
3. p(n):=1; q(n):=num(a(n)/a(n-1)); r(n):=den(a(n)/a(n-1));
4. while (Res(n,q(n),r(n+j)) má nezáporný celý kořen j=j0) do
g(n):=gcd(q(n),r(n+j0));
q(n):=q(n)/g(n);
r(n):=r(n)/g(n-j0);
p(n):=p(n)g(n)g(n-1)...g(n-j0+1);
od;
5. lp:=deg(q(n+1)+r(n));
lm:=deg(q(n+1)-r(n));
if lp <= lm then k:=deg(p(n))-lm
else
k0:=2 (-lp cof(q,lp)-cof(q,lp-1)+cof(r,lp-1))/
(cof(q,lp)+cof(r,lp));
if (k0 je celé) then k:=max(k0,deg(p(n))-lp+1)
else k:=deg(p(n))-lp+1;
fi
fi;
if k < 0 then b:=false; return fi;
6. vyřešit rekurentní vzorec p(n)=q(n+1)f(n)-r(n)f(n-1)
s okrajovou podmínkou f(1)=p(1)/q(2)
pro f(n)=ck n^k+...+c0
if (neexistuje řešení) then b:=false; return fi;
7. S(n):=q(n+1)a(n)f(n)/p(n);
return