Vektory a matice

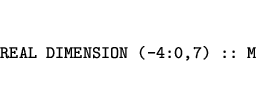
S částmi matic lze nyní manipulovat podobně jako v Matlabu. Máme-li matici o 5 řadách a 7 sloupcích

$$\begin{eqnarray*} &&\mbox{\tt REAL DIMENSION (-4:0,7) :: M} \end{eqnarray*}$$

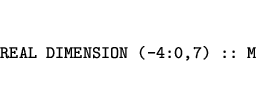
vybere M(-3,:) druhou řadu, zatímco M(0:-4:-2,1:7:2) vezme překlopenou submatici

$$\begin{eqnarray*} {\tt\left[ \begin{array}{llll} M_{0,1} & M_{0,3} & M_{0,5} &... ... M_{-4,1} & M_{-4,3} & M_{-4,5} & M_{-4,7} \end{array}\right] } \end{eqnarray*}$$

Příkaz RESHAPE změní tvar matice při zachování počtu a hodnot prvků:

$$\begin{eqnarray*} &&\mbox{\tt REAL DIMENSION (6) :: VEKTOR} \\ &&\mbox{\tt REAL... ... 8, 6 /)} \\ &&\mbox{\tt MATICE = RESHAPE( VEKTOR, (/ 2,3 /) )} \end{eqnarray*}$$

Běžné skalární operace se provádějí po prvcích:

$$\begin{eqnarray*} &&\mbox{\tt REAL DIMENSION (5,20) :: X,Y}\\ &&\mbox{\tt REAL ... ...mbox{~~~~~~~~}{\tt\vdots} \\ &&\mbox{\tt Z = 2.0 * Y * SQRT(X)} \end{eqnarray*}$$

Chybě, způsobené v předchozím příkladu negativním prvkem matice X, zabráníme konstruktem WHERE:

$$\begin{eqnarray*} &&\mbox{\tt WHERE (X >= 0.0)}\\ &&\mbox{~~~~{\tt Z = 2.0 * Y ... ...SEWHERE}\\ &&\mbox{~~~~{\tt Z = 0.0}}\\ &&\mbox{\tt END WHERE} \end{eqnarray*}$$

Kontrolní otázka: Musí být ELSEWHERE psáno jako jedno slovo?

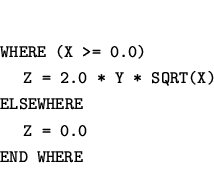
Nově Fortran 90 umožňuje i čistě maticové operace. Jsou to mimo jiné:

Jméno funkce	Vrací
MAXVAL(A)	hodnotu největšího prvku
MINVAL(A)	hodnotu nejmenšího prvku
MAXLOC(A)	indexy největšího prvku
MINLOC(A)	indexy nejmenšího prvku
SUM(A)	součet hodnot prvků
PRODUCT(A)	součin hodnot prvků
MATMUL(A,B)	maticový součin
DOT_PRODUCT(A,B)	skalární součin vektorů
TRANSPOSE(A)	transponovanou matici
CSHIFT(A,POSUN,DIMENZE)	cyklicky posunutou matici

Chceme-li sečíst pouze kladné prvky matice X, použijeme masku

$$\begin{eqnarray*} &&\mbox{\tt SOUCET = SUM(X, MASK = X > 0.0)} \end{eqnarray*}$$

Obrázek 1: Cyklický posun matice.

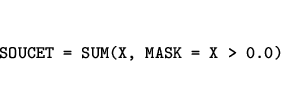
Přestavění matice cyklickou záměnou je schematicky znázorněno na obr. 1. Pokud neuvedeme jinak, posouvá se podle dimenze 1. Že se jedná o poměrně silný nástroj, dokazuje následující příklad. To, co bychom ve Fortranu 77 museli opsat smyčkou

      REAL A(0:99), B(0:99)
      DO 1000, I=0,99
        B(I) = ( A(MOD(I+99,100) + A(MOD(I+1,100) )/2 
1000  CONTINUE

můžeme ve Fortranu 90 zkrátit na

      REAL A(100), B(100)
      B = ( CSHIFT(A,+1) + CSHIFT(A,-1) )/2