

Next: Semiimplicitní Eulerova metoda
Up: Stiff rovnice (rovnice se
Previous: Stiff rovnice (rovnice se
Uvažujeme pro jednoduchost jen jednu rovnici 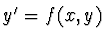 ,
která má hladké řešení
,
která má hladké řešení 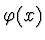 . Spočítáme numericky řešení
. Spočítáme numericky řešení
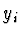 v bodech
v bodech 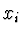 . Chceme, aby pro
. Chceme, aby pro
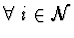 byla chyba
byla chyba
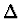 numerického řešení omezená
numerického řešení omezená
Dosadíme do diferenciální rovnice
Odtud pro derivaci chyby platí
Přibližně můžeme brát 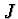 jako konstantní a pak
jako konstantní a pak
kde 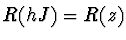 je dáno metodou numerického řešení diferenciální rovnice.
Pro Eulerovu metodu je
je dáno metodou numerického řešení diferenciální rovnice.
Pro Eulerovu metodu je 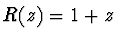 . Aby bylo
. Aby bylo
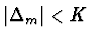 pro
pro
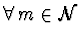 , musí být
, musí být 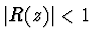 . Pro Eulerovu metodu
musí být
. Pro Eulerovu metodu
musí být
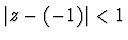 .
.
Pro systém rovnic je chyba vektor 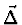 a jeho derivace je dána
maticí J. Je tedy
a jeho derivace je dána
maticí J. Je tedy
Nechť J není defektní a existuje tedy pro
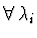 ,
,
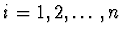 vlastní vektor
vlastní vektor 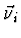 . Potom lze vyjádřit
. Potom lze vyjádřit
Pak lze chybu v 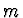 -tém kroku zapsat ve tvaru
-tém kroku zapsat ve tvaru
Pak chyba je omezená v limitě
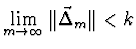 právě
tehdy, když pro
právě
tehdy, když pro
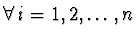 je, že
je, že
Z této podmínky mohu najít maximální krok 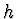 takový, že absolutní chyba
metody nebude postupně narůstat (metoda je stabilní pro daný krok).
takový, že absolutní chyba
metody nebude postupně narůstat (metoda je stabilní pro daný krok).
Pozn. Pro
Eulerovu metodu je
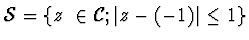 .
.
Def. Metoda je A-stabilní, jestliže je
Pozn. A-stabilní metoda je stabilní pro 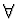 délky kroku
délky kroku 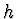 .
.
Implicitní Eulerova metoda je A-stabilní.
Zde
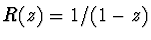 a tedy
a tedy 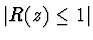 na množině (vnějšek kruhu)
na množině (vnějšek kruhu)
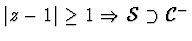 .
.
Pozn. V praxi se obvykle užívají implicitní metody vyššího řádu.


Next: Semiimplicitní Eulerova metoda
Up: Stiff rovnice (rovnice se
Previous: Stiff rovnice (rovnice se
Jiri Limpouch
2000-05-25
![]() ,
která má hladké řešení
,
která má hladké řešení ![]() . Spočítáme numericky řešení
. Spočítáme numericky řešení
![]() v bodech
v bodech ![]() . Chceme, aby pro
. Chceme, aby pro
![]() byla chyba
byla chyba
![]() numerického řešení omezená
numerického řešení omezená
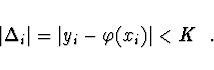
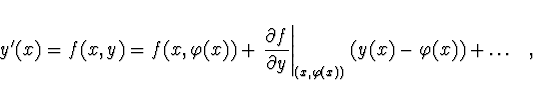
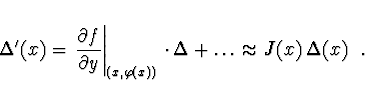
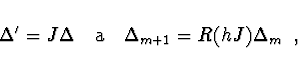
![]() a jeho derivace je dána
maticí J. Je tedy
a jeho derivace je dána
maticí J. Je tedy
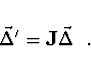
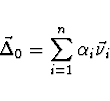
![\begin{displaymath}
\vec{\Delta}_m = \sum \limits_{i=1}^n \left[ R(h \lambda_i)
\right]^m \alpha_i \vec{\nu}_i \ \ .
\end{displaymath}](img267.gif)
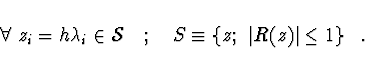
![]() .
.
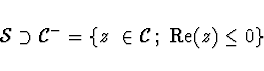
![]() délky kroku
délky kroku ![]() .
.
![]() a tedy
a tedy ![]() na množině (vnějšek kruhu)
na množině (vnějšek kruhu)
![]() .
.