Konvergence vícekrokových metod

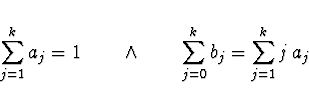
Konzistence - Vícekroková metoda je konzistentní, pokud je alespoň 1. řádu přesnosti.
Metoda je konzistentní právě tehdy, jestliže

$$\sum \limits_{j=1}^k a_j = 1 \qquad \wedge \qquad \sum \limits_{j=0}^k b_j = \sum \limits_{j=1}^k j\, a_j$$

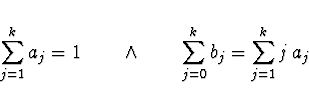
Vícekroková metoda

$$y_{i+1} = \sum \limits_{j=1}^k a_j y_{i+1-j} + h \sum \limits_{j=0}^k b_j f_{i+1-j}\ \ .$$

má charakteristický polynom

$$\lambda^k - a_1 \lambda^{k-1} - \dots - a_k = 0\ \ .$$

Pokud je metoda konzistentní, pak je alespoň jeden kořen $\lambda_1 = 1$.

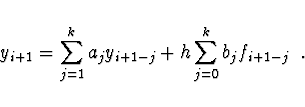
D-stabilní metoda (stabilní v limitě kroku $h \rightarrow 0$), má $\forall \, i = 1, \dots, m$ vlastní čísla (kořeny charakteristického polynomu) $\vert\lambda_i\vert \leq 1$ a ty, pro které je $\vert\lambda_i\vert = 1$, jsou jednoduché kořeny.

Pozn. Každá konzistentní metoda má jeden z kořenů charakteristického polynomu $\lambda = 1$.

Věta Pokud je vícekroková metoda konzistentní a D-stabilní, pak je konvergentní.

Pozn. Adamsovy metody jsou D-stabilní, mají charakteristický polynom
$\lambda^k - \lambda^{k-1} = 0$, tedy $\lambda_1 = 1$ a $\lambda_2 = \dots = \lambda_m = 0$.