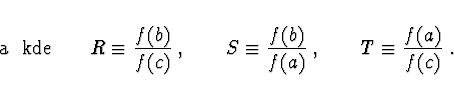Metody je založena na přepínání mezi lineární metodou
(metodou půlení intervalů) a superlineární metodou (inverzní
kvadratická interpolace). Pokud je superlineární metoda pomalá
(daleko od kořene), využívá se půlení intervalů.
Inverzní kvadratická interpolace využívá funkci ![]() ,
hledáme
,
hledáme ![]() . Při iteraci z 3 známých
bodů
. Při iteraci z 3 známých
bodů ![]() , je funkce
, je funkce ![]() interpolována
podle Lagrangeova vzorce
interpolována
podle Lagrangeova vzorce
![$\displaystyle \frac{[y - f(a)][y - f(b)]c}{[f(c) - f(a)][f(c) - f(b)]} +$](img49.gif) |
|||
![$\displaystyle \frac{[y - f(b)][y - f(c)]a}{[f(a) - f(b)][f(a) - f(c)]} +
\frac{[y - f(c)][y - f(a)]b}{[f(b) - f(c)][f(b) - f(a)]}\ \ .$](img51.gif) |
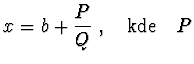 |
|||