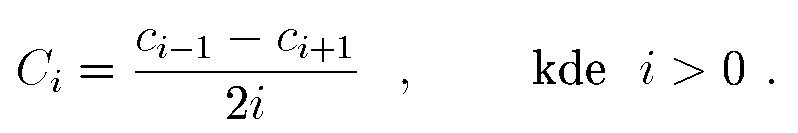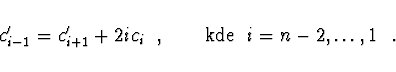Aproximace Čebyševovými polynomy se lehce konstruuje a je téměř
tak přesná jako nejlepší stejnoměrná aproximace.
Často se používá pro výpočet funkcí.
Pro interpolaci Čebyševovými polynomy se libovolný interval
lineárně transformuje na interval
![]() Každému
Každému
![]() přiřadíme hodnotu
přiřadíme hodnotu
![]() funkčním předpisem
funkčním předpisem
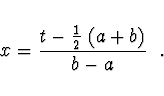
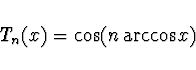
Polynomy 0-tého a 1-ního stupně jsou tedy ![]() a
a ![]() .
Čebyševův polynom
.
Čebyševův polynom ![]() -tého stupně lze též vyjádřit pomocí
rekurentního vztahu
-tého stupně lze též vyjádřit pomocí
rekurentního vztahu
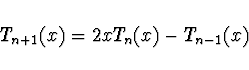
Pomocí rekurentního vztahu lze odvodit tvar dalších Čebyševových polynomů
Kořeny a extrémy
Čebyševův polynom ![]() má
má ![]() kořenů v intervalu
kořenů v intervalu
![]() v bodech
v bodech
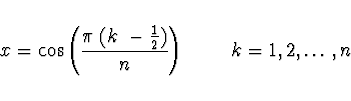
Ortogonalita
Čebyševovy polynomy jsou ortogonální polynomy
s vahou
![]() na intervalu
na intervalu
![]()
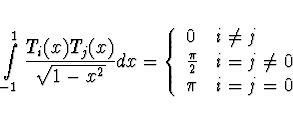
Diskrétní ortogonalita
Nechť ![]() ,
,
![]() jsou
kořeny Čebyševova polynomu
jsou
kořeny Čebyševova polynomu ![]() . Pak pro
. Pak pro
![]() platí
platí
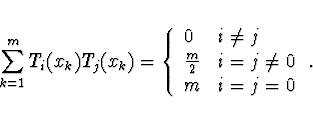
Aproximace Čebyševovými polynomy
Funkci ![]() aproximujeme
aproximujeme
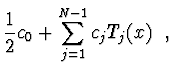 |
|||
![$\displaystyle \frac{2}{N} \sum_{k=1}^{N} f \left[ \cos \left( \frac{\pi
(k~-\fr...
...{2})}{N} \right) \right] \cos \left( \frac{\pi j (k~-
\frac{1}{2})}{N} \right).$](img244.gif) |
Hodnoty funkce ![]() jsou rovny hodnotám funkce
jsou rovny hodnotám funkce ![]() ve všech
ve všech
![]() nulových bodech polynomu
nulových bodech polynomu ![]() .
.
Výpočet funkce pomocí Čebyševových polynomů
Často volíme pro výpočet koeficientů relativně vysoký řád
aproximace
![]() (procedura CHEBFT v knihovně Numerical Recipies).
Koeficienty Čebyševova rozvoje jdou obvykle
(procedura CHEBFT v knihovně Numerical Recipies).
Koeficienty Čebyševova rozvoje jdou obvykle ![]() relativně
rychle. Vysoké
relativně
rychle. Vysoké ![]() dovoluje přesně stanovit počet členů potřebných
pro výpočet funkce se zadanou přesností
dovoluje přesně stanovit počet členů potřebných
pro výpočet funkce se zadanou přesností ![]() .
Pokud je
.
Pokud je
![]() ,
potom pro výpočet funkce stačí použít prvních
,
potom pro výpočet funkce stačí použít prvních ![]() členů rozvoje
(procedura CHEBEV v knihovně Numerical Recipies).
členů rozvoje
(procedura CHEBEV v knihovně Numerical Recipies).
Pozn. Počítání Lagrangeova polynomu s body danými nulovými body
Čebyševova polynomu je možné, ale pro ![]() je méně přesné a
obtížnější.
je méně přesné a
obtížnější.
Pozn. Procedura CHEBEV používá pro sumu funkcí zadaných
rekurentně používá Clenshawovy formule.
Pokud je řada funkcí dána rekurentně
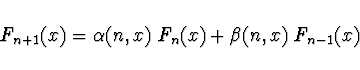
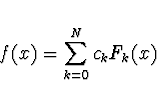
Integrál a derivace pomocí Čebyševových polynomů
Koeficienty ![]() Čebyševova rozvoje integrálu funkce
Čebyševova rozvoje integrálu funkce ![]() jsou dány
jsou dány