Construction of doubly periodic solutions via the Poincare-Lindstedt method in the case of massless 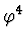$\varphi ^4$ theory.

O. A. Khrustalev¹
Institute for Theoretical Problems of Microphysics,
Moscow State University,
Department of Physics, Moscow State University,
Moscow, 119899, Russia

and

S. Yu. Vernov²
Institute of Nuclear Physics, Moscow State University,
Moscow, 119899, Russia

Full paper in compressed Postscript *.ps.gz

Abstract:

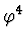
Doubly periodic (periodic both in time and in space) solutions for the Lagrange-Euler equation of the (1+1)-dimensional scalar $\varphi ^4$theory are studied. Provided that nonlinear term is small, the Poincare-Lindstedt asymptotic method is used to find asymptotic solutions in the standing wave form. It is proved that using the Jacobi elliptic function cn as the zero approximation one can solve the problem of the main resonance, appearing in the case of zero mass, and construct a uniform expansion.