We consider Toeplitz, Hankel, Vandermonde and Cauchy matrices as well as the matrices having similar structures. These are the most popular classes of dense structured matrices, omnipresent in scientific, engineering and electrical engineering computations. For readers convenience, we recall the definitions (cf. [BP94], [PCZ,a]).
Toeplitz matrices are a special class (where ![]() of the following important and well-studied class of Toeplitz-like
matrices having a small displacement rank
r (cf. [BP94], pp. 174-211).
of the following important and well-studied class of Toeplitz-like
matrices having a small displacement rank
r (cf. [BP94], pp. 174-211).
where
is a down-shift
where G and H are
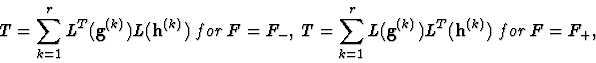 where
where
![]()
![]() and
and ![]() is a lower triangular Toeplitz
matrix with the first column
is a lower triangular Toeplitz
matrix with the first column ![]() .
.
Hankel matrices and the Hankel-like matrices
of displacement rank r are
obtained from Toeplitz matrices and Toeplitz-like matrices of
displacement rank r ,
respectively, by their
pre-multiplication (or post-multiplication) by the reflection
matrix
J having ones on its antidiagonal and zero entries elsewhere. (Note that
![]() is the identity matrix.)
is the identity matrix.)
where
Note that Vandermonde and Cauchy matrices have scaling/displacement and scaling ranks 1, respectively.
We also recall the next well-known results [BP94].
Dut to Theorem 6.1 and equations (6.1)-(6.3), Theorem 6.2 is immediately extended to Toeplitz-like, Hankel-like, Vandermonde-like and Cauchy-like matrices.
As this was shown in
[P89/90], some computations with dense structured matrices
of the above four classes can be conveniently reduced to each other, so that
any successful algorithm for some fundamental
computations
for matrices
of one class
can be effectively extended
to the matrices of the other three classes.
In [GKO95], [Hei95]
such a reduction from Toeplitz and Toeplitz-like matrices to Cauchy-like matrices
was simplified and exploited to yield an effective practical
algorithm for fast and
numerically stable solution of Toeplitz and Toeplitz-like linear
systems of n equations by Gaussian elimination with pivoting
(at the cost ![]() )), and surely, this is immediately extended to the Hankel
and Hankel-like linear systems.
The main point of this approach is that the row and/or column
interchange destroys the structure of Toeplitz-like and Hankel-like
matrices (which either blocks the application of pivoting
in Gaussion elimination or slows down the computation) but
preserves the Cauchy-like matrix structure.
The latter property of Cauchy-like matrices can be observed either from matrix equation
(6.5) or from the following equivalent representation,
)), and surely, this is immediately extended to the Hankel
and Hankel-like linear systems.
The main point of this approach is that the row and/or column
interchange destroys the structure of Toeplitz-like and Hankel-like
matrices (which either blocks the application of pivoting
in Gaussion elimination or slows down the computation) but
preserves the Cauchy-like matrix structure.
The latter property of Cauchy-like matrices can be observed either from matrix equation
(6.5) or from the following equivalent representation,
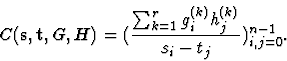
Another known approach to solving Toeplitz-like and Hankel-like linear systems
of equations as well
as to the computation of short displacement generators of the inverses of
![]() Toeplitz, Hankel, Toeplitz-like and Hankel-like matrices, in all cases
at the cost
Toeplitz, Hankel, Toeplitz-like and Hankel-like matrices, in all cases
at the cost ![]() ,
is by the divide-and-conquer MBA algorithm of [M80], [BA80].
,
is by the divide-and-conquer MBA algorithm of [M80], [BA80].
The algorithm relies on the following well-known factorization of
![]() block matrices,
block matrices,
where I and O denote the identity and null matrices of appropriate sizes, B is a
For a strongly nonsingular
matrix A , the factorization (6.7)-(6.9)
can be extended to the matrices B and S and then recursively to the matrices of smaller
size until we arrive at ![]() matrices. The important point
is to preserve the structure of the input matrix A throughout the recursive process, which enables the
application of Theorem 6.2 and
respective decrease of the
computational time to the cited level
matrices. The important point
is to preserve the structure of the input matrix A throughout the recursive process, which enables the
application of Theorem 6.2 and
respective decrease of the
computational time to the cited level ![]() .
The algorithm of [M80], [BA80]
achieved this goal for Toeplitz-like
matrices.
.
The algorithm of [M80], [BA80]
achieved this goal for Toeplitz-like
matrices.
By using the reduction of [P89/90] from
Cauchy-like to Toeplitz-like matrices, the latter cost estimate can
be extended to the Cauchy-like case. Such a reduction, however,
is more involved than the reduction into the opposite direction
(from Toeplitz-like to Cauchy-like matrices),
and its numerical properties are not clear. In
[PZ96], [PTCPS98] and [OP98],
the divide-and-conquer algorithm based on(6.7)-(6.9)
was devised directly for the Cauchy-like inversion and the solution of
Cauchy-like linear systems of equations, at the cost
![]() (cf. Theorem 6.2).
In [OP98], the algorithm
was also applied to some major problems of rational
interpolation, which are the basis for some
fundamental signal processing computations
and which can be expressed as the
recursive factorization problem based on (6.7)-(6.9).
The main technicality of the extension of the MBA algorithm is the extension to
the Cauchy-like case
of the results of [M80], [BA80] on
maintaining the Toeplitz-like structure throughout the recursive factorization
process.
(cf. Theorem 6.2).
In [OP98], the algorithm
was also applied to some major problems of rational
interpolation, which are the basis for some
fundamental signal processing computations
and which can be expressed as the
recursive factorization problem based on (6.7)-(6.9).
The main technicality of the extension of the MBA algorithm is the extension to
the Cauchy-like case
of the results of [M80], [BA80] on
maintaining the Toeplitz-like structure throughout the recursive factorization
process.
If the inverses of the dense structured matrices of the above classes are computed numerically, with some bounded output errors due to roundoff, then the output approximations can be very rapidly refined by Newton's iteration. Straightforward application of such an iteration causes rapid growth of the length of the displacement or scaling generators and a slowdown of the computations as a results, but some nontrivial modifications avoid this problem [P92a], [P93], [PZHD97], [PBRZ,a].
The basic block of all these algorithms is the multiplication of a dense
structured matrix of a given class by a vector (cf. Theorem
6.2 on the complexity of such a multiplication). In the Cauchy-like case, we have the reduction to the
problem of multiplication of a Cauchy matrix by a vector, also known as
Trummer's celebrated problem, having various applications to
scientific and engineering computing (see bibliography in [PTCLS98]).
By Theorem 6.2, its solution cost is bounded by ![]() ,
but the algorithm of [Ger87] supporting this bound is numerically
unstable. For numerical solution of Trummer's problem, the methods of
practical choice are the multipole algorithms (cf. [Rok85],
[Ger87], [AGR88], [GR87], [War98]), which are numerically stable and
compute an approximate solution of Trummer's problem at the cost
,
but the algorithm of [Ger87] supporting this bound is numerically
unstable. For numerical solution of Trummer's problem, the methods of
practical choice are the multipole algorithms (cf. [Rok85],
[Ger87], [AGR88], [GR87], [War98]), which are numerically stable and
compute an approximate solution of Trummer's problem at the cost ![]() where
where ![]() bounds the output error norm.
bounds the output error norm.
The cited transitions among various classes of structured matrices have
some interesting applications to polynomial computations. In particular,
recall that polynomial interpolation and multipoint evaluation can be
expressed as the computation of the vector ![]() for a given pair of
vectors
for a given pair of
vectors ![]() and
and ![]() and of the vector
and of the vector ![]() for a given pair of
vectors
for a given pair of
vectors ![]() and
and ![]() ,
respectively, where the three vectors
,
respectively, where the three vectors ![]() ,
,
![]() and
and ![]() of the same dimension n satisfy the vector equation
of the same dimension n satisfy the vector equation
and
The known fast algorithms yield the cost bound ![]() for both problems but are numerically unstable. The similarity with
Trummer's problem can be continued from this point; furthermore, we
reduce polynomial interpolation and multipoint evaluation to Trummer's
problem based on the next equation (such a reduction was first proposed
in [PLST93], [PZHY97]; cf. also [PTCLS98], [PTCPS98]):
for both problems but are numerically unstable. The similarity with
Trummer's problem can be continued from this point; furthermore, we
reduce polynomial interpolation and multipoint evaluation to Trummer's
problem based on the next equation (such a reduction was first proposed
in [PLST93], [PZHY97]; cf. also [PTCLS98], [PTCPS98]):
Here