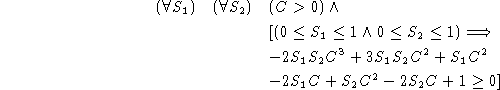![]()
where ![]() is a general quantifier (for all) or
existential quantifier (there exists) and
is a general quantifier (for all) or
existential quantifier (there exists) and ![]() is a
logical combination of polynomial equations and inequalities in
the variables
is a
logical combination of polynomial equations and inequalities in
the variables ![]()
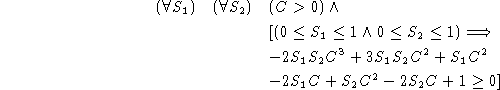
![]()
where ![]() is a general quantifier (for all) or
existential quantifier (there exists) and
is a general quantifier (for all) or
existential quantifier (there exists) and ![]() is a
logical combination of polynomial equations and inequalities in
the variables
is a
logical combination of polynomial equations and inequalities in
the variables ![]()