Resultant

 

• let be polynomials with coefficients from the domain

• the domain can be e.g., integers or polynomials in other variables

  
  
  

• the Sylvester matrix of polynomials is the matrix

  
  
  

• where rows are constructed from the coefficients of the polynomial and rows from the coefficients of the polynomial

• the resultant of the polynomials and with respect to the variable , denoted by , is the determinant of the Sylvester matrix

• using the special structure of the Sylvester matrix, we can calculate the resultant by the following recursive algorithm

• Algorithm

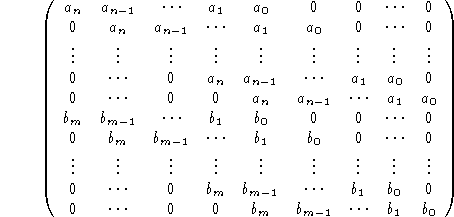
        res := RES(x, a, b) :=
          [a, b are polynomials
           algorithms used:
             rem(a, b) - remainder after dividing a by b
             deg(a)    - degree of the polynomial a
             lcof(a)   - leading coefficient of the polynomial a, i.e., the
                         coefficient of x^deg(a)]
        1. n := deg(a)
           m := deg(b)
        2. if n > m then res :=(-1)^(n m) RES(x, b, a)
             else lc := lcof(a)
                  if n = 0 then res := lc^m
                    else r := rem(b, a)
                         if r = 0 then res := 0
                           else p := deg(r)
                                res := lc^(m - p) RES(x, a, r)
                         fi
                  fi
           fi

• this algorithm gradually replaces rows in the Sylvester matrix derived from the coefficients of the polynomial by rows derived from the coefficients of the remainder ; these new rows are computed as linear combinations of the rows of the original matrix

• after the above replacement, the matrix has only zeroes below the diagonal in its first columns while the diagonal has the values ; the matrix block consisting of the last rows and columns is the Sylvester matrix of the polynomials ; thus, in general case of the algorithm, we can use the formula