

Next: Representation of algebraic structures
Up: Algebraic structures
Previous: Number domains
- ring of polynomials
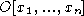 in
in  variables with operations of addition, subtraction,
multiplication and exponentiation by a nonnegative integer; see
the examples of polynomials ; polynomial coefficients can be numbers from
a number domain
variables with operations of addition, subtraction,
multiplication and exponentiation by a nonnegative integer; see
the examples of polynomials ; polynomial coefficients can be numbers from
a number domain
- power series, other kinds of series
- rational functions
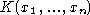 (extension of
polynomials by the operation of division) with operations of
addition, subtraction, multiplication, division and exponentiation
by an integer; see the examples of rational functions
(extension of
polynomials by the operation of division) with operations of
addition, subtraction, multiplication, division and exponentiation
by an integer; see the examples of rational functions
- extension of rational functions by radicals (rational exponents),
with operations of addition, subtraction, multiplication,
division and exponentiation by a rational number
- algebraic functions
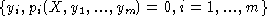 implicitly defined by polynomials with integer coefficients
implicitly defined by polynomials with integer coefficients
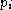 which depend on algebraic functions
which depend on algebraic functions 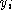 and variables from
and variables from 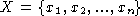 , e.g.,
the algebraic function
, e.g.,
the algebraic function 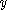 defined by the polynomial
defined by the polynomial
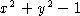
- elementary transcendental functions
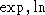 ,
extension of rational functions by elementary transcendental
functions; if we have only one variable
,
extension of rational functions by elementary transcendental
functions; if we have only one variable  and an
expression contains
and an
expression contains 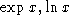 , we can denote
, we can denote
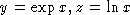 and work with a rational function of
and work with a rational function of
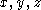 -- the extension is given only by rules
like
-- the extension is given only by rules
like 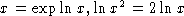 , etc.
, etc.
- transcendental functions: e.g.,
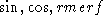 ;
extension of rational functions by transcendental functions
;
extension of rational functions by transcendental functions
- matrix rings
- differential fields
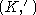
- finite groups
- a user can use algebraic expressions from an arbitrary domain for
the most part; the program will decide which domain the
expression belongs in and use an appropriate algorithm
Richard Liska