Položme ![]() a
a
![]() . Vložíme mezi
. Vložíme mezi ![]() a
a ![]() body
body
![]() . Budeme hledat aproximaci řešení v uvedených bodech.
Nejjednodušší je ekvidistantní krok
. Budeme hledat aproximaci řešení v uvedených bodech.
Nejjednodušší je ekvidistantní krok
![]() . Derivace lze nahradit
konečnými diferencemi různě.
Například
. Derivace lze nahradit
konečnými diferencemi různě.
Například
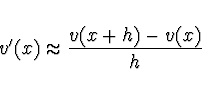
![\begin{displaymath}
v'(x) - \left[ \frac{v(x + h) - v(x)}{h} \right] = \frac{1}{2}
v''(x) h + O(h^2) ,
\end{displaymath}](img303.gif)
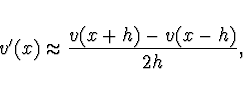
![\begin{displaymath}
v'(x) - \left[ \frac{v(x + h) - v(x - h)}{2h} \right] = -
\frac{h^2}{3!} v'''(x) h + O(h^4).
\end{displaymath}](img305.gif)
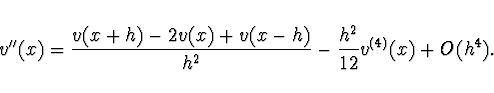
Ukázka pro lineární diferenciální rovnici
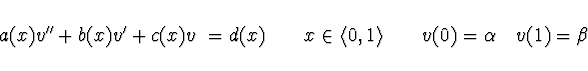
Tuto rovnici lze pro všechna
![]() aproximovat diferenční rovnicí
aproximovat diferenční rovnicí
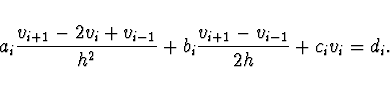
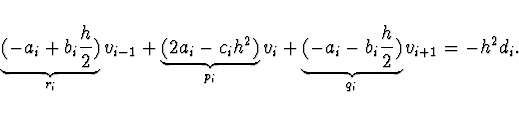
![\begin{displaymath}
\left[
\begin{array}{ccccccc}
p_1 & q_1 & 0 & & \dots & & 0 ...
...\\ d_{n-1} \\
d_n + q_n \frac{\beta}{h^2}
\end{array}\right].
\end{displaymath}](img312.gif)
Lze dokázat, že pokud ![]() , pak pro
, pak pro
![]() platí
platí
![]() .
.
Pozn. Pokud okrajové podmínky obsahují derivace, musíme je
též aproximovat. Ke zvýšení řádu této aproximace často užíváme
virtuálních bodů ![]() a
a ![]() .
.
Pozn. Při řešení okrajových úloh pro obyčejné diferenciální rovnice metodou sítí je nutno řešit systémy lineárních rovnic s pásovou maticí.