Gaussovy kvadratury

Chceme spočítat integrál s minimálním počtem vyčíslení funkce $f(x)$. Volíme optimální polohu bodů $x_i$ a váhy jednotlivých bodů $w_i$. Gaussova metoda s použitím $N$ bodů dává přesný výsledek pro $\forall$ polynomy řádu $2N-1$, čili dvojnásobek řádu (přesnosti) integrace s ekvidistantním dělením. Řád metody se tak zvýší z $N$ na $2N$. Polohy a váhy bodů jsou známy pro i pro integrace s některými vahami $W(x)$.
Jde o integrál

$$\int \limits_a^b W(x) f(x)\, {\rm d}x \approx \sum \nolimits_{i=1}^N W_i f(x_i)\ \ ,$$

kde funkce $f(x)$ by měla být hladká, relativně málo proměnná.

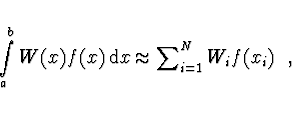
Z Hermiteovy interpolace vyplývá, že body $x_i$ musí být vybrány tak, aby polynom

$$\omega_N (x) = \prod_{i=1}^N (x - x_i)$$

byl ortogonální ke $\forall$ polynomům stupně nejvýše $N-1$ ve skalárním součinu daném integrálem s příslušnou vahou. Body $x_i$ jsou tedy kořeny příslušného ortogonálního polynomu řádu $N$.

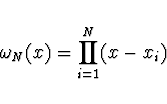
Často se používají tyto polynomy:

$(a, b)$	$W(x)$	Druh polynomů	Rekurenční vztah
$(-1,1)$	$1$	Legendrovy	$P_{i+1} = \frac{2i+1}{i+1} x P_i - \frac{i}{i+1} P_{i-1}$
$(-1,1)$	$\frac{1}{\sqrt{1-x^2}}$	Čebyševovy	$T_{i+1} = 2x T_i - T_{i-1}$
$(0,+\infty)$	$x^c e^{-x}$	Laguerrovy ( $c = 0, 1, \dots$)	$L_{i+1}^c = \frac{2i +c +1 - x}{i +1} L_i^c - \frac{i+c}{i+1} L_{i-1}^c$
$(-\infty, +\infty)$	$e^{-x^2}$	Hermiteovy	$H_{i+1} = 2x H_i - 2i H_{i-1}$

Mluvíme pak o Gauss-Legendreově, Gauss-Čebyševově ...integraci. Tabulky vah a $x_i$ najdeme v literatuře, například: Abramowitz, M. A., Stegun, I. A., Handbook of Mathematical Functions. Příslušné procedury najdeme v numerických knihovnách.