Hledáme maximum účinkové funkce ![]() , úloha je zadána následovně
, úloha je zadána následovně
Nyní sestavíme proměnné do tabulky, ![]() jsou levostranné
proměnné a
jsou levostranné
proměnné a ![]() pravostranné.
pravostranné.
| |
|
||
|
|
0 | 2 | -4 |
|
|
2 | -6 | 1 |
|
|
8 | 3 | -4 |
Kdyby ![]() mělo všechny koeficienty u pravostranných proměnných
menší nebo rovné nule, byla by úloha již vyřešená. Kladné
koeficienty u pravostranných proměnných v
mělo všechny koeficienty u pravostranných proměnných
menší nebo rovné nule, byla by úloha již vyřešená. Kladné
koeficienty u pravostranných proměnných v ![]() je třeba odstranit.
Vybereme tu pravostrannou proměnnou (sloupec), která má u z maximální
kladný koeficient. Pro tuto proměnnou vybereme hlavní prvek -
podmínku (řádek), která maximálně omezuje rozsah proměnné a z této
podnínky proměnnou vyjádříme, zde
je třeba odstranit.
Vybereme tu pravostrannou proměnnou (sloupec), která má u z maximální
kladný koeficient. Pro tuto proměnnou vybereme hlavní prvek -
podmínku (řádek), která maximálně omezuje rozsah proměnné a z této
podnínky proměnnou vyjádříme, zde
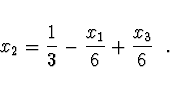
| |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Maximum ![]() je tedy při
je tedy při ![]() ,
, ![]() ,
, ![]() a
a ![]() .
.
Algoritmus řešení lze tedy shrnout