Metoda konjugovaných gradientů pro řešení systému lineárních rovnic s pozitivně definitní maticí

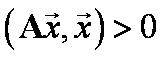Úlohou je řešit , kde A je pozitivně definitní matice, tj. symetrická matice definující pozitivně definitní kvadratickou formu a tedy pro

Nechť je přesné řešení úlohy. Pak funkce 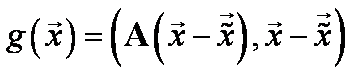má ^{minimum rovné 0 pro}

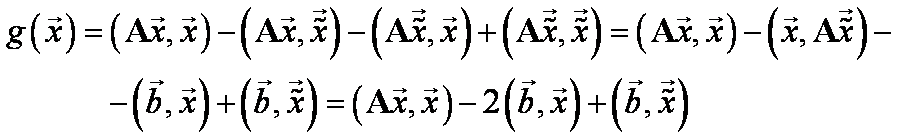
Poslední člen je konstanta (byť neznámá) a proto ho lze vynechat.

^{Proto i funkce 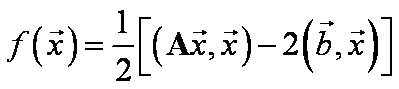má minimum pro}

Systém lineárních rovnic řešíme nalezením minima 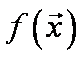metodou konjugovaných gradientů

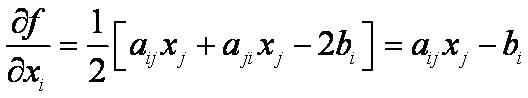^{a tedy}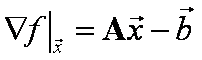

Počáteční odhad je a 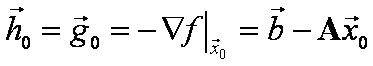, při iteracích 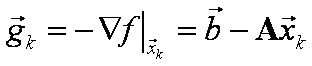^a ,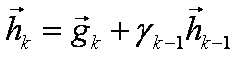

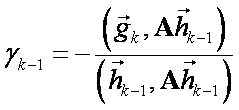
^{Minimalizací ve směru dostaneme 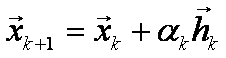, funkci vyjádříme}

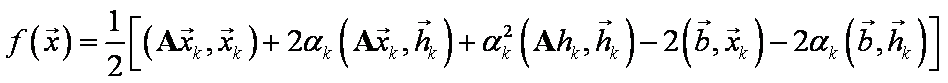
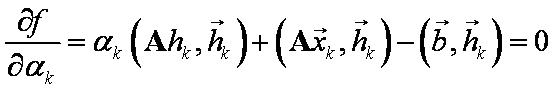a tedy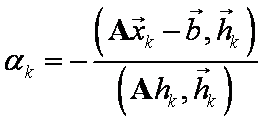

a tak k nalezení minima ve směru - násobení vektoru maticí a skal.součin

Pro řídké matice je násobení vektoru maticí velmi rychlé (řádu N a ne N²)