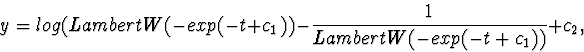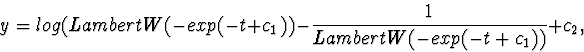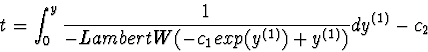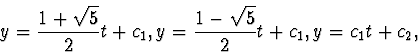Examples

The following examples were found with the help of the system Maple V Release 4.

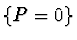
EXAMPLE 3   Let P=P(y,y⁽¹⁾,exp(Q₁))=y⁽¹⁾-exp(y⁽¹⁾-y), where Q₁=y⁽¹⁾-y. By using the command dsolve there is no answer to dsolve(P=0,y). If z= exp(Q₁), then the equation $\{P=0\}$ is equivalent to the system
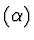
$(\alpha)$={y⁽¹⁾-z=0, z⁽¹⁾-y⁽²⁾+y⁽¹⁾=0, y⁽²⁾-z⁽¹⁾=0, z= exp(y⁽¹⁾-y)}.
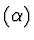
By eliminating z, the system $(\alpha)$ is equivalent to the system
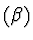
$(\beta)$={y⁽¹⁾-z=0, z⁽¹⁾-y⁽²⁾+y⁽¹⁾=0, P₁=-y⁽²⁾+y⁽¹⁾y⁽²⁾-(y⁽¹⁾)²=0, z= exp(y⁽¹⁾-y)}.
By using the command dsolve, dsolve(P₁=0,y) gives the answer

$$y=log(LambertW(-exp(-t+c_{1}))-\frac{1}{LambertW(-exp(-t+c_{1}))}+c_{2},$$

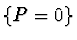
where c₁,c₂ are arbitrary constants and LambertW is a solution of the equation yexp(y)-t=0. The solutions of $\{P=0\}$ are given by substituting y and its derivatives in P=0 by the corresponding solutions of P₁=0 in order to find conditions on the constants, because there is only one constant in the general solution of P=0.

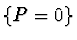
EXAMPLE 4   Let P=P(y,y⁽¹⁾,log(R₁))=y⁽¹⁾-log(y⁽¹⁾-y), where R₁=y⁽¹⁾-y. By using the command dsolve there is no answer to dsolve(P=0,y). If v= log(R₁), then the equation $\{P=0\}$ is equivalent to the system
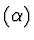
$(\alpha)$={y⁽¹⁾-v=0, y⁽¹⁾v⁽¹⁾-yv⁽¹⁾-y⁽²⁾+y⁽¹⁾=0, y⁽²⁾-v⁽¹⁾=0, v= log(y⁽¹⁾-y)}.
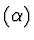
By eliminating v, the system $(\alpha)$ is equivalent to the system
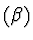
$(\beta)$={y⁽¹⁾-v=0, y⁽¹⁾v⁽¹⁾-yv⁽¹⁾-y⁽²⁾+y⁽¹⁾=0, P₁= -y⁽²⁾+y⁽¹⁾+y⁽¹⁾y⁽²⁾-yy⁽²⁾)=0, v= log(y⁽¹⁾-y)}.
By using the command dsolve, dsolve(P₁=0,y) gives the answer

$$t=\int^{y}_{0} \frac{1}{-LambertW(-c_{1}exp(y^{(1)})+y^{(1)})}dy^{(1)}-c_{2}$$

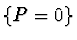
where c₁,c₂ are arbitrary constants and LambertW is a solution of the equation yexp(y)-t=0. The solutions of $\{P=0\}$ are given by substituting y and its derivatives in P=0 by the corresponding solutions of P₁=0 in order to find conditions on the constants, because there is only one constant in the general solution of P=0.

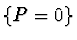
EXAMPLE 5   Let P= P(y,y⁽¹⁾,exp(Q₁),log(R₁))= y⁽¹⁾-y-exp(y⁽¹⁾)- log(y⁽¹⁾), where Q₁=y⁽¹⁾ and R₁=y⁽¹⁾. By using the command dsolve there is no answer to dsolve(P=0,y). If z= exp(Q₁) and v= log(R₁), then the equation $\{P=0\}$ is equivalent to the system
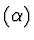
$(\alpha)$={ y⁽¹⁾-y-z-v=0, z₁-y⁽²⁾=0, y⁽¹⁾v⁽¹⁾-y⁽²⁾=0, y⁽²⁾-y⁽¹⁾-z⁽¹⁾-v⁽¹⁾=0, z= exp(y⁽¹⁾), v= log(y⁽¹⁾)}.
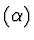
By eliminating v and z, the system $(\alpha)$ is equivalent to the system
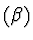
$(\beta)$={y⁽¹⁾-v=0, z₁-y⁽²⁾=0, y⁽¹⁾v⁽¹⁾-y⁽²⁾=0, P₁= y⁽¹⁾y⁽²⁾z-y⁽¹⁾y⁽²⁾+(y⁽¹⁾)²+y⁽²⁾=0, P₁⁽¹⁾=0, P₂= (y⁽²⁾)³+(y⁽²⁾)³y⁽¹⁾-(y⁽²⁾)²(y⁽¹⁾)² -(y⁽²⁾)³(y⁽¹⁾)²+(y⁽²⁾)²(y⁽¹⁾)³+ y⁽³⁾(y⁽¹⁾)³}.
By using the command dsolve, dsolve(P₂=0,y) gives the answer

y=exp((texp(c)+Ei(-exp(c))c₁esp(c)-1+c₂exp(x))exp(-c)+c₃,

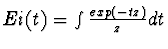
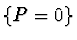
where c₁,c₂,c₃ are arbitrary constants and $Ei(t)= \int \frac{exp(-tz)}{z}dt$. The solutions of $\{P=0\}$ are given by substituting y and its derivatives in P=0 by the corresponding solutions of P₁=0 in order to find conditions on the constants, because there is only one constant in the general solution of P=0.

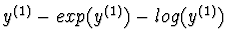
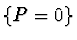
EXAMPLE 6   Let P= P(y,y⁽¹⁾,exp(Q₁),log(R₁))= $y^{(1)}-exp(y^{(1)})-\\ log(y^{(1)})$, where Q₁=y⁽¹⁾ and R₁=y⁽¹⁾. By using the command dsolve there is no answer to dsolve(P=0,y). If z= exp(Q₁) and v= log(R₁), then the equation $\{P=0\}$ is equivalent to the system
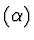
$(\alpha)$={ y⁽¹⁾-z-v=0, z₁-y⁽²⁾=0, y⁽¹⁾v⁽¹⁾-y⁽²⁾=0, y⁽²⁾-z⁽¹⁾-v⁽¹⁾=0, z= exp(y⁽¹⁾),v= log(y⁽¹⁾)}.
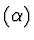
By eliminating v and z, the system $(\alpha)$ is equivalent to the system
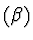
$(\beta)$={y⁽¹⁾-v=0, z₁-y⁽²⁾=0, y⁽¹⁾v⁽¹⁾-y⁽²⁾=0, P₁= y⁽¹⁾y⁽²⁾z-y⁽¹⁾y⁽²⁾+y⁽²⁾=0, P₁⁽¹⁾=0, P₂=-(y⁽²⁾)³-(y⁽²⁾)³y⁽¹⁾+(y⁽²⁾)³(y⁽¹⁾)²}.
By using the command dsolve, dsolve(P₂=0,y) gives the answer

$$y=\frac{1+\sqrt{5}}{2}t+c_{1}, y=\frac{1-\sqrt{5}}{2}t+c_{1}, y=c_{1}t+c_{2},$$

where c₁,c₂ are arbitrary constants. By using the comand fsolve, fsolve(x-exp(x)-log(x),x) gives the answer x=0.3441612867.
So y=0.3441612867t+c₂ is the general solution of {P=0}.