COMPUTATION AND APPLICATIONS OF THE NEWTON POLYHEDRON
Alexander B. Aranson
Department of Mathematics, Keldysh Institute of Applied Mathematics
Miusskaja Square 4, Moscow 125047, Russia
gtrtp@glasnet.ru, aranson@spp.keldysh.ru
Abstract
We consider the multidimensional polynomial
where
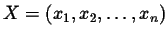 ,
,
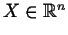 or
or
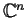 ,
,
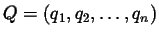 ,
,
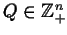 ,
,
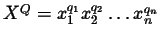 is a monomial,
coeficients
is a monomial,
coeficients
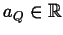 or
or 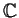 and D is some set
in
and D is some set
in
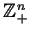 .
The set
.
The set
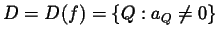 is called the support of the
polynomial f(X). The convex hull M=M(f) of the set D is called
the Newton polyhedron of the polynomial f(X).
There is some correspondence between properties of the polynomial f(X)
and of its Newton polyhedron M(f).
It was studied by Bruno, Soleev, Khovanskiy and somes other.
We propose algorithms and the computer programm for computation of the
Newton polyhedron of any multidimensional polynomial, and for computation
of all elements of this polyhedron (surfaces, vertices, edges, etc.).
We consider the application of the Newton polyhedron method for analysis
of the behavior of a 4-dimensional reversible ODE system near its equilibrium
point. This system appeared from Hydrodynamics after reduction on the center
manifold of the water-wade problem.
is called the support of the
polynomial f(X). The convex hull M=M(f) of the set D is called
the Newton polyhedron of the polynomial f(X).
There is some correspondence between properties of the polynomial f(X)
and of its Newton polyhedron M(f).
It was studied by Bruno, Soleev, Khovanskiy and somes other.
We propose algorithms and the computer programm for computation of the
Newton polyhedron of any multidimensional polynomial, and for computation
of all elements of this polyhedron (surfaces, vertices, edges, etc.).
We consider the application of the Newton polyhedron method for analysis
of the behavior of a 4-dimensional reversible ODE system near its equilibrium
point. This system appeared from Hydrodynamics after reduction on the center
manifold of the water-wade problem.
IMACS ACA'98 Electronic Proceedings