Shigekazu Nakagawa
![]() ,
Hiroki Hashiguchi
,
Hiroki Hashiguchi
![]() ,
Naoto Niki
,
Naoto Niki
![]()
![]() Kurashiki University of Science and the Arts
Kurashiki University of Science and the Arts
![]() Science University of Tokyo
Science University of Tokyo
Formally speaking, the definition of the zonal polynomials is
as follows.
Let
![]() be the set of all partitions of the non-negative
integer n no longer than
be the set of all partitions of the non-negative
integer n no longer than ![]() ,
,
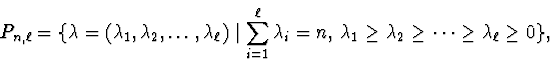
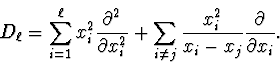
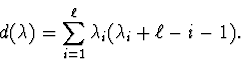
For a fixed basis of symmetric polynomials,
![]() is uniquely expressed under some regular conditions.
For example,
if
is uniquely expressed under some regular conditions.
For example,
if
![]() runs through all partitions in
runs through all partitions in
![]() then
then
![]() forms a basis where
forms a basis where
![]() are
fundamental symmetric polynomials
are
fundamental symmetric polynomials
![]() .
If we take such
.
If we take such
![]() as a basis then
as a basis then
![]() can be expressed
can be expressed
![\begin{displaymath}z(\lambda) = \sum_{\mu \in P_{n,\ell}} c[\lambda, \mu]e(\mu^{\prime}),\end{displaymath}](img19.gif)
The problem is to find
![]() for given
for given ![]() and develop a symbolic algorithm to determine them.
The key is simplifying
and develop a symbolic algorithm to determine them.
The key is simplifying ![]() ,
that is,
finding a simple expression of
,
that is,
finding a simple expression of ![]() in terms of
in terms of
![]() .
The relevant problem is for the case
.
The relevant problem is for the case
![]() while a symbolic algorithm based on a recurrence formula is well-known
for the case
while a symbolic algorithm based on a recurrence formula is well-known
for the case
![]() .
.
In this paper, we give
a simplification for the Laplace-Beltrami operator for any ![]() .
Moreover, for
.
Moreover, for ![]() we give
a symbolic algorithm including
sufficient conditions that the coefficients vanish
to determine the coefficients of zonal polynomials.
we give
a symbolic algorithm including
sufficient conditions that the coefficients vanish
to determine the coefficients of zonal polynomials.